Пред.   След.

Формулы

Модель сети

При движении теплоносителя по паропроводу его параметры (давление, температура и др.) меняются вдоль трубы. Эти изменения связаны с охлаждением теплоносителя через стенку и теплоизоляцию трубы, а также с потерей давления из-за трения. На некотором расстоянии от источника пар может стать влажным (двухфазное состояние теплоносителя) и в этом случае температура и давление не определяют однозначно состояние теплоносителя. Привлекать третий параметр влажность либо степень сухости пара не слишком удобно, более естественно выбрать в качестве динамических переменных давление и энтальпию. Эти переменные однозначно определяют состояние теплоносителя, в том числе температуру и влажность. В общем случае, уравнение, описывающее изменение давления и энтальпии вдоль трубы можно записать в виде:

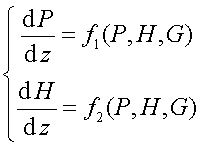
Рисунок 193.


В качестве параметра здесь присутствует массовый расход (конкретный вид функций в правых частях уравнений будет приведен позже). Для определения массовых расходов во всех трубах нужно решить уравнения Кирхгофа первого и второго рода. Первый из них утверждает, что алгебраическая сумма расходов, втекающих в узел, равна нулю (вытекающие расходы входят в эту сумму со знаком минус). Второй закон Кирхгофа гласит, что сумма изменений давления по всем участкам, образующим замкнутый цикл, равна нулю.

Таким образом, чтобы из дифференциальных уравнений найти давления нужно знать расходы, а чтобы решить алгебраические уравнения Кирхгофа с целью отыскания расходов нужно знать давления. Чтобы выйти из этого «заколдованного» круга, естественно применить метод последовательных приближений при котором поочередно решаются система алгебраических уравнений, а затем система дифференциальных уравнений.

Начальные условия для дифференциальных уравнений определяются последовательно, начиная с труб, выходящих из источников пара. Для других труб начальные условия для давлений вычисляются из уравнений Кирхгофа, а начальная энтальпия для трубы по которой теплоноситель вытекает из узла, вычисляется как средневзвешенная энтальпия по всем расходам втекающим в этот узел, причем в качестве весов выступают расходы:

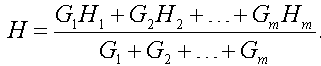
Рисунок 194.


Основные этапы построения решения

Дифференциальные уравнения решаются численно методом Рунге-Кутта.

Чтобы выписать уравнения Кирхгофа для произвольной трубопроводной сети целесообразно привлечь теорию графов.

Топология трубопроводной сети моделируется с помощью ориентированного графа, причем дуги графа соответствуют участкам труб и элементам, имеющим гидравлическое сопротивление, а вершины графа соответствуют концам труб (и точкам их соединения).

Пусть A - матрица инцидентности (точнее базисная подматрица матрицы инцидентности, которая получается из полной матрицы инцидентности в результате отбрасывания какой-нибудь строки - обычно последней). Тогда первый закон Кирхгофа, утверждающий, что сумма расходов, втекающих и вытекающих в любой узел равна нулю, можно записать в виде матричного уравнения

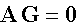
Рисунок 195.


Для записи второго закона Кирхгофа используется матрица базисных циклов В. Эту матрицу можно получить в результате следующей процедуры. Выберем какое-нибудь остовное дерево графа (для ускорения процессов сходимости итерационных процессов решения нелинейных уравнений Кирхгофа рекомендуется выбирать дерево с наименьшим гидравлическим сопротивлением). Выбор остовного дерева (базисного минора матрицы инцидентности) разбивает дуги графа на ветви и хорды, при этом соответствующие расходы разбиваются на базисные и свободные. С учетом этого разбиения уравнение первый закон Кирхгофа можно переписать в виде:

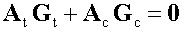
Рисунок 196.


Здесь At и Ac - квадратная и прямоугольная матрицы, составленные соответственно из базисных столбцов (индекс t от английского слова tree - древо) и остальных (индекс с от английского слова chord - хорда).

Выразим базисные переменные через свободные:

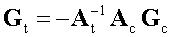
Рисунок 197.


Можно показать, что матрица базисных циклов, соответствующая выбранному остовному дереву имеет вид:

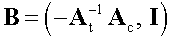
Рисунок 198.


Второй закон Кирхгофа, утверждающий, что сумма падений давления, с учетом действующих напоров, по любому замкнутому контуру равна нулю, можно записать в виде:

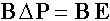
Рисунок 199.


Здесь 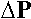- матрица-столбец, составленная из падений давления на каждом из участков трубопроводной сети, E матрица-столбец, составленная из действующих напоров на каждом из участков трубопроводной сети.

Уравнение (1.7) является нелинейным даже в простейшем случае гидравлической сети (в случае гидравлической сети при решении нелинейных уравнений помогает метод Ньютона). В случае паропроводов компоненты векторы 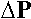определяются из решения системы дифференциальных уравнений, причем решения не являются гладкими функциями. Излом решения образуется в точке появления конденсата. С учетом этих замечаний для решения нелинейных уравнений применим метод минимизации невязок. Введем вектор невязок (residual vector)

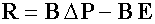
Рисунок 200.


и вычислим норму, например евклидову (в конечномерном случае все нормы эквивалентны), этого вектора:

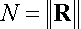
Рисунок 201.


Течение пара по трубе

Одномерное стационарное, неизотермическое движение пара по трубе описывается фундаментальными уравнениями: первое начало термодинамики (закон сохранения энергии), уравнение изменения количества движения (уравнение движения), уравнение неразрывности (закон сохранения массы):

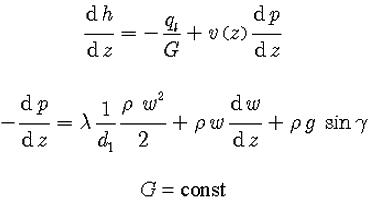
Рисунок 202.


здесь:

  • h – энтальпия;

  • p – давление;

  • z – координата, направленная вдоль трубы;

  • ql – линейная плотность теплового потока от газа к воздуху;

  • G – массовый расход;

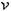  • – удельный объем газа;

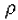  • – плотность газа;

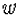  • – скорость движения газа;

  • d1 – внутренний диаметр трубы;

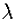  • – коэффициент гидравлического трения (безразмерный);

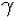  • – угол наклона трубы;

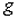  • – ускорение свободного падения.

Рисунок 203.


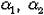– коэффициенты теплоотдачи соответственно от пара к внутренней стенке трубы и от наружной поверхности изоляции к воздуху, Вт/м2К.

Теплофизические свойства пара

Для вычисления теплофизических свойств (энтальпия, температура, влажность, плотность, энтропия, кинематическая вязкость и др.) пара и воды привлекается программа WaterSteamPro (http://www.wsp.ru/ru/), которая основана на системе уравнений IAPWS-IF97, предложенной в 1997 г. Международной ассоциацией по свойствам воды и водяного пара и предназначенной для промышленных расчетов.