Проекция


Пред.		След.

Поверхность земли имеет сферическую форму, поэтому приходится каким-то образом изображать реальный мир в плоской или планарной системе координат. При создании карт эллипсоид вращения должен быть развернут на плоскость. Понятно, что он не может быть развернут на плоскости без складок или разрывов, поэтому при создании карт прибегают к помощи картографических проекций, в которых отображение поверхности земли или иного небесного тела происходит по строгим математическим законам. Эти законы выражают функциональную связь координат точек на поверхности эллипсоида вращения и плоскости (карте). В основу такого отображения положена система географических или геодезических координат, координатными линиями которой являются меридианы и параллели.

Различные проекции имеют разные типы искажений. Некоторые проекции разработаны с учетом минимизации искажений одной или двух характеристик данных. Проекция может сохранять площадь объектов, но изменять их форму. Растяжение и сжатие отдельных частей изображения картографируемой поверхности в той или иной проекции неизбежно сопровождается искажениями длин, площадей и углов. В одних проекциях можно избежать искажения углов, в других – площадей, но длины линий будут искажены во всех проекциях, за исключением отдельных точек или некоторых линий на карте, о чем мы поговорим несколько позже.

Картографические проекции предназначены для определенных целей. Так, некоторые картографические проекции могут использоваться для отображения крупномасштабных объектов на ограниченной площади, другие – для составления мелкомасштабных карт мира.

Проекции классифицируются по следующим основным признакам:

по характеру искажений;
по виду нормальной сетки параллелей и меридианов;
по ориентировке вспомогательной поверхности.

По характеру искажений различают проекции:

Равновеликие – в них отсутствует искажение площадей. Значительны искажения углов и форм. Такие проекции часто используются для землеустроительных целей, измерения площадей и картографирования плотности населения, а также для исследований одной определённой области.
Равноугольные – в них отсутствует искажения углов, вследствие этого в них не искажаются формы фигур, а масштаб длин в любой точке остается одинаковым по всем направлениям. В этих проекциях карты больших территорий отличаются значительным искажением площадей. Весьма удобны для решения навигационных задач. Угол на местности всегда равен углу на карте; линия прямая на местности, прямая на карте. Главным примером данной проекции является поперечно-цилиндрическая Проекция Меркатора (1569 г.); она до сих пор используется для морских навигационных карт.
Произвольные – в них имеются искажения и углов, и площадей, но в значительно меньшей степени, чем в равновеликих и равноугольных проекциях, поэтому они используются чаще всего.

Среди них особое место занимают равнопромежуточные проекции, в которых масштаб длин по одному из главных направлений сохраняется постоянным.

По по виду нормальной сетки параллелей и меридианов различают проекции:

Конические – это проекции, в которых поверхность эллипсоида переносится на боковую поверхность касательного к нему (а) или секущего его конуса (б), а затем последний разрезается по образующей его линии и развертывается в плоскость. В конических проекциях параллели – это дуги одноцентренных окружностей, а меридианы – прямые линии, сходящиеся в одной точке (полюсе) под углами, пропорциональными разности долгот (в). В таких проекциях искажения не зависят от долготы. Особо пригодны для территорий, вытянутых вдоль параллелей. Карты всей территории СССР часто составляются в равноугольных и равнопромежуточных конических проекциях.

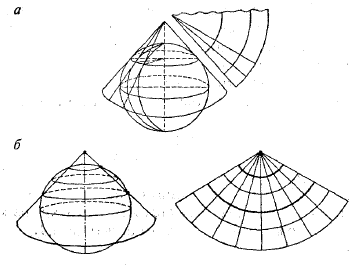
Рисунок 31. Коническая проекция
Цилиндрические – это проекции, в которых происходит проектирование земной поверхности на боковую поверхность цилиндра, которая потом разворачивается в плоскость. Цилиндр может быть касательным к земному шару или секущим его. В первом случае длины сохраняются по экватору. Во втором – по двум стандартным параллелям.

Цилиндрические проекции бывают прямые, косые и поперечные. В прямых цилиндрических проекциях одни и те же участки поверхности изображаются одинаково вдоль линии разреза в восточной и западной частях карты, что обеспечивает удобство чтения карты по широтным поясам. Косые цилиндрические проекции имеют географическую сетку, которая дает представление о сферичности земного шара. С уменьшением широты полюса кривизна параллелей увеличивается, а их протяженность уменьшается, что дает представление о сферичности земли.

Цилиндрические проекции применяются при составлении карт мелких и крупных масштабов – от общегеографических до специальных. Так, например, аэронавигационные маршрутные полетные карты чаще всего составляются в косых и поперечных цилиндрических равноугольных проекциях (на шаре).

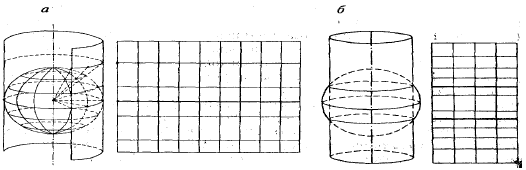
Рисунок 32. Цилиндрическая проекция
Азимутальные – проекции, в которых параллели нормальной сетки есть концентрические окружности, а меридианы – их радиусы, расходящиеся из общего центра параллелей под углами, равными разности долгот. Каждая точка на карте имеет тот же самый азимут по отношению к среднему меридиану, который эта же точка имеет со средним меридианом на сфере. Название азимутальных проекции получили благодаря основному их свойству сохранять без искажений азимуты линий, выходящих из точки касания картинной плоскости.

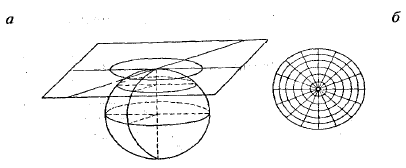
Рисунок 33. Азимутальная проекция

Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор которой зависит от расположения территории. Меридианы и параллели в косых и поперечных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор: он является второй осью симметрии.
Псевдоконические – проекции, у которых параллели изображаются дугами концентрических окружностей, один из меридианов, называемый средним, – прямой линией, а остальные – кривыми, симметричными относительно среднего. Примером псевдоконической проекции может служить равновеликая псевдоконическая проекция Бонна.
Псевдоцилиндрические – проекции, в которых все параллели изображаются параллельными прямыми, средний меридиан – прямой линией, перпендикулярной параллелям, а остальные меридианы – кривыми. При этом средний меридиан является осью симметрии проекции. Псевдоцилиндрические проекции в основном применяются для изображения всей земной поверхности или значительных ее частей в мелких масштабах. По этой причине земная поверхность принимается за поверхность шара с радиусом R. Эти проекции имеют две оси симметрии – экватор и средний меридиан нормальной сетки. Косые и поперечные псевдоцилиндрические проекции используются крайне редко.