Описание элементов
(при достаточно большой площади поверхности воды
в резервуаре). Уровень воды в резервуаре за время моделирования переходных
процессов успевает измениться незначительно, поэтому граничное условие на конце
отводной трубы имеет вид 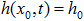 .
.
описывается с учетом двух характеристик: насоса и скважины. В процессе отыскания начальных условий определяются расход G и уровень воды в скважине H с учетом формулы
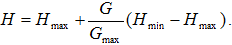
Рисунок 498. (26)
Здесь 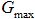 – производительность скважины,
– производительность скважины, 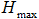 – уровень воды в скважине при нулевом расходе,
– уровень воды в скважине при нулевом расходе, 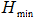 – уровень воды в скважине при максимальном расходе. Далее,
если во время переходного процесса расход уменьшается, то уровень воды в
скважине не увеличивается, поскольку предполагается, что скважина обладает
большой инерционностью. Наоборот, если во время переходного процесса расход
увеличивается на
– уровень воды в скважине при максимальном расходе. Далее,
если во время переходного процесса расход уменьшается, то уровень воды в
скважине не увеличивается, поскольку предполагается, что скважина обладает
большой инерционностью. Наоборот, если во время переходного процесса расход
увеличивается на 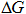 , то уровень воды в скважине уменьшается на величину
, то уровень воды в скважине уменьшается на величину 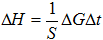 , где
, где 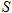 – площадь поперечного сечения скважины,
– площадь поперечного сечения скважины, 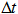 – величина шага по времени.
– величина шага по времени.
с фиксированным отбором описывается граничным
условием вида 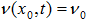 . Следует понимать, что такая модель весьма грубая.
. Следует понимать, что такая модель весьма грубая.
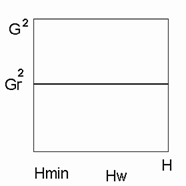
Рисунок 499. Потребитель с фиксированным отбором
с заданным напором описывается таким же
граничным условием, как и резервуар 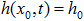 , пока расход положителен, и условием
, пока расход положителен, и условием 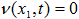 , как только расчет приводит к отрицательному значению
расхода, т. е. потребитель не может быть источником.
, как только расчет приводит к отрицательному значению
расхода, т. е. потребитель не может быть источником.
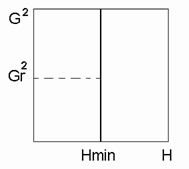
Рисунок 500. Потребитель с заданным напором
с ограниченным (нефиксированным) отбором
описывается либо граничным условием вида 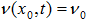 (в случае, когда потребителю хватает напора), либо
граничным условием типа заданного сопротивления
(в случае, когда потребителю хватает напора), либо
граничным условием типа заданного сопротивления 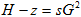 (в противном случае). Здесь z – геодезическая отметка, H –
пьезометрический напор, (H-z) – избыточное давление в метрах водяного
столба. Сопротивление задается либо вычисляется по формуле
(в противном случае). Здесь z – геодезическая отметка, H –
пьезометрический напор, (H-z) – избыточное давление в метрах водяного
столба. Сопротивление задается либо вычисляется по формуле 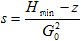 , где
, где 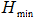 – минимальный напор, требуемый потребителем,
– минимальный напор, требуемый потребителем, 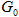 – номинальный расход, требуемый потребителем.
– номинальный расход, требуемый потребителем.
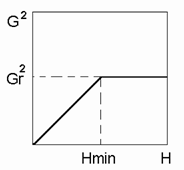
Рисунок 501. Потребитель с ограниченным (нефиксированным) отбором
с истечением воды через отверстие описывается
граничным условием вида 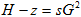 . Здесь z – геодезическая отметка, H –
пьезометрический напор, (H-z) – избыточное давление в метрах водяного
столба. Сопротивление задается либо вычисляется по формуле
. Здесь z – геодезическая отметка, H –
пьезометрический напор, (H-z) – избыточное давление в метрах водяного
столба. Сопротивление задается либо вычисляется по формуле 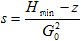 , где
, где 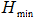 – минимальный напор, требуемый потребителем,
– минимальный напор, требуемый потребителем, 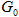 – номинальный расход, требуемый потребителем.
– номинальный расход, требуемый потребителем.
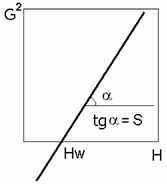
Рисунок 502. Потребитель с истечением воды через отверстие
это узел, в котором соединяются две или более труб. Сложное соединение труб приводит к граничным условиям
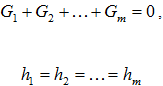
Рисунок 503. (27)
Сумма расходов втекающих в узел равна нулю, а давления (напоры) равны потому, что измеряются в одной точке.
описывается следующими граничными условиями для концов трех труб (труба до колпака, труба после колпака и соединительный патрубок между магистралью и колпаком)
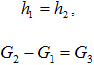
Рисунок 504. (28)
Здесь 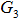 – расход жидкости, втекающей в воздушный колпак, и он
зависит от разности давлений (и соответственно напоров) жидкости в месте
соединения колпака с трубой и воздуха внутри колпака
– расход жидкости, втекающей в воздушный колпак, и он
зависит от разности давлений (и соответственно напоров) жидкости в месте
соединения колпака с трубой и воздуха внутри колпака
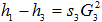
Рисунок 505. (29)
Давление внутри колпака находится из уравнения состояния газа (изотерма 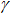 =1, адиабата
=1, адиабата 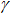 =1.4 или политропа
=1.4 или политропа 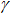 =1.2.
=1.2.
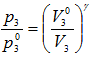
Рисунок 506. (30)
Здесь 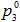 и
и 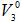 – давление и объем воздуха в начальный момент времени.
Наконец, для отыскания объема
– давление и объем воздуха в начальный момент времени.
Наконец, для отыскания объема 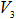 имеем уравнение
имеем уравнение
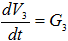
Рисунок 507. (31)
которое приходится решать численно, поскольку зависимость 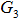 от времени не известна. Отметим, что воздушный колпак можно
использовать для моделирования воздушного пузыря в трубе.
от времени не известна. Отметим, что воздушный колпак можно
использовать для моделирования воздушного пузыря в трубе.
(задвижка, вентиль и пр.) Наличие задвижки приводит к граничным условиям
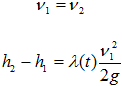
Рисунок 508. (32)
Здесь 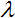 (
(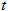 ) – безразмерный коэффициент сопротивления задвижки. Для
каждого конкретного типа задвижки коэффициент сопротивления можно выразить через
степень закрытия задвижки, а зависимость последнего от времени задает
пользователь, например, можно задать время начала закрытия, продолжительность
процесса и назначить линейную зависимость степени закрытия от времени.
) – безразмерный коэффициент сопротивления задвижки. Для
каждого конкретного типа задвижки коэффициент сопротивления можно выразить через
степень закрытия задвижки, а зависимость последнего от времени задает
пользователь, например, можно задать время начала закрытия, продолжительность
процесса и назначить линейную зависимость степени закрытия от времени.
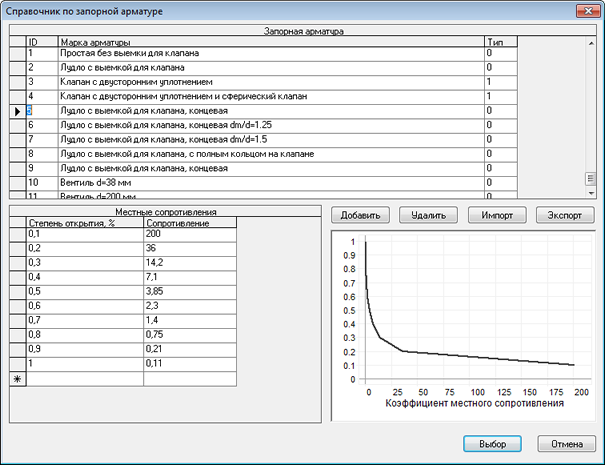
Рисунок 509. Справочник по запорной арматуре
Отметим, что в программе имеются справочники по задвижкам (смотрите рисунок) и насосам, что позволяет пользователю либо выбрать устройство из справочника либо добавить в список новое устройство и ввести характеристику табличным способом.
H описывается граничными условиями
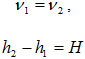
Рисунок 510. (33)
Эта грубая модель предполагает, что электропривод насоса имеет бесконечную мощность.
. В этом случае напор
H ,
развиваемый насосом и его к. п. д. 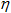 зависят от расхода G. Соответствующие характеристики
приводятся заводом-изготовителем насоса. Для удобства пользователей к ZuluGIS
подключается справочник с некоторым набором насосов (смотрите рисунок). Как
правило, завод-изготовитель приводит
зависят от расхода G. Соответствующие характеристики
приводятся заводом-изготовителем насоса. Для удобства пользователей к ZuluGIS
подключается справочник с некоторым набором насосов (смотрите рисунок). Как
правило, завод-изготовитель приводит 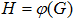 и
и 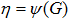 характеристики насоса только для одной номинальной частоты
вращения ротора. Поэтому, в процессе решения характеристики пересчитываются для
произвольной частоты вращения, используя свойства подобия
характеристики насоса только для одной номинальной частоты
вращения ротора. Поэтому, в процессе решения характеристики пересчитываются для
произвольной частоты вращения, используя свойства подобия 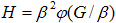 и
и 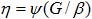 . Тогда граничные условия примут вид
. Тогда граничные условия примут вид
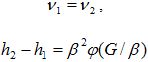
Рисунок 511. (34)
Расход очевидным образом выражается через скорость течения жидкости 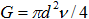 .
.
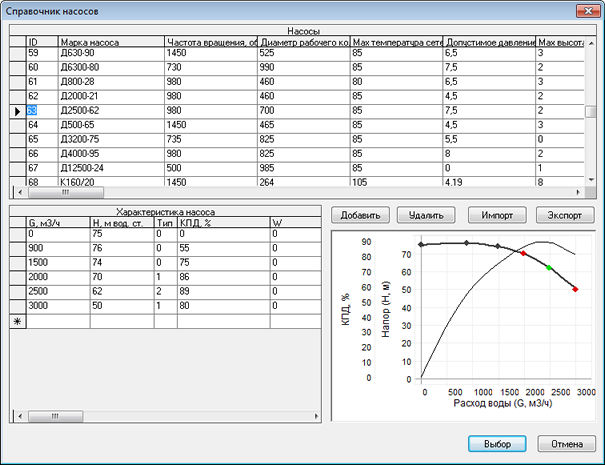
Рисунок 512. Справочник по насосам
Изменение частоты вращения в свою очередь описывается уравнением движения 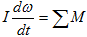 .
.
Здесь I – момент инерции агрегата насос - ротор электродвигателя, в сумму моментов входят: вращающий момент электродвигателя, момент сопротивления жидкости и момент трения. Разрушаемая мембрана не влияет на процессы в сети, пока она не разрушена. После достижения давления разрешения, в точке подключения разрушаемой мембраны происходит свободное истечение жидкости, которое моделируется известными уравнениями с заданным сопротивлением. Отметим, что элемент «разрушаемая мембрана» можно использовать для моделирования аварийной ситуации – разрушение трубы.
(например, фильтр) описывается уравнениями
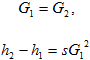
Рисунок 513. (35)
в течение переходного процесса моделируется локальным сопротивлением, т. е. мы полагаем, что инерционность регулятора давления велика. Это локальное сопротивление подбирается во время стационарного расчета, определяющего начальные условия.
представляет собой небольшое локальное сопротивление при течении жидкости в одном направлении
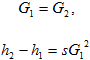
Рисунок 514. (36)
и бесконечное сопротивление при течении жидкости в другом направлении, что
приводит к граничным условиям 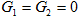 . Инерционными свойствами обратного клапана мы пренебрегаем.
. Инерционными свойствами обратного клапана мы пренебрегаем.