Выше приведены примеры простейших переходных процессов при различных возмущениях. Обратим внимание на некоторые очевидные особенности графиков.

В первом примере каждая «полуволна» соответствует времени пробега волны сжатия или разрежения от задвижки до резервуара и обратно. Легко подсчитать среднюю скорость распространения звуковых волн. Имеем 13.5 полуволн, расстояние туда и обратно 400 метров, время 4 секунды. Таким образом, средняя скорость равна 13.5 *400/4=1350 м/сек. Как видим, скорость распространения волн мало отличается от скорости звука в воде без примеси воздуха 1425 м/сек. Объясняется это тем, что содержание нерастворенного воздуха в воде задано весьма малым, а толщина стенок труб слишком большой - 1см. При уменьшении толщины стенок труб до 1мм скорость распространения волн снижается до 1000 м/сек. Увеличение содержания нерастворенного воздуха в воде также приводит к значительному снижению скорости распространения волн сжатия.

Однако самое сильное влияние на скорость звука оказывает величина давления - при очень низких давлениях скорость может упасть до 20 м/сек.

По поводу величины повышения давления при закрытии задвижки можно заметить, что та величина, которую мы видим на экране (около 88 метров) хорошо согласуется с предсказанием по формуле Жуковского 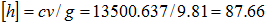Скорость течения жидкости v можно взять из среднего графика после вычисления начальных условий, а более точные значения записаны в базе данных по участкам.

Теперь по поводу других примеров. Во втором и четвертом примерах существенного повышения давления не наблюдается. Но следует понимать, что при наличии пузырей воздуха в конце трубопровода возможно катастрофическое повышение давления. Возможность моделирования таких ситуаций предусмотрена в нашей программе.